TRINOMIO DE SEGUNDO GRADO

Trinomio de Segundo Grado" (o "Séptimo Caso")

1/3 x² - 1/3 x + 1/12 = 1/3. (x - 1/2).(x - 1/2) = 1/3. (x - 1/2)²

Cuando aplico la "fórmula de la cuadrática", obtengo un sólo resultado. Es que en realidad el Trinomio es "cuadrado perfecto", y podría factorizarse por el Tercer Caso, pero aplicando primero el caso Factor Común (en este ejemplo en particular). 

Explicación:

Uso la fórmula "resolvente" de las ecuaciones cuadráticas, para encontrar los valores de x₁ y x₂ 

x_1,2 = 

Y para nuestro ejemplo a = 1/3, b = -1/3 y c = 1/12 (1/3 x² - 1/3x + 1/12). Entonces, reemplazo en la fórmula, y me queda: 

x_{1,2 =} 

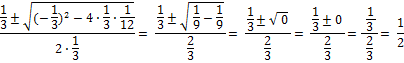
x₁ = x₂ =  1/2    

Como "lo que está debajo de la raíz" me dió cero, y raíz de cero es cero, por más que sume o reste 0 obtendré el mismo resultado: 1/2. Entonces hay un solo resultado, una sola raíz para este polinomio. Se la llama "raíz doble". Y cuando sucede esto es porque el trinomio de segundo grado que queremos factorizar es en realidad un trinomio cuadrado perfecto, y hubiera sido mejor que lo factorizáramos con el Tercer Caso: Trinomio Cuadrado Perfecto

Luego tengo que factorizar el polinomio según la fórmula:

a.(x - x₁).(x - x₂)

Donde a = 1/3 es el coeficiente principal del polinomio (el número que multiplica a la x²). Y x₁ y x₂ son las "raíces" del polinomio de segundo grado, que hallé con la fórmula de la ecuación cuadrática. Pero en este ejemplo en particular, x₁ y x₂ resultaron ser iguales a 1/2. Así tengo que reemplazar en esa fórmula a "a", x₁ y x₂ con los valores que encontré:

1/3.(x - 1/2).(x - 1/2) =

a             x₁            x₂ 

Pero como quedaron dos (x - 1/2) multiplicándose, puedo poner en lugar de ambos: (x - 1/2)² que es lo mismo que (x - 1/2).(x - 1/2). Entonces, la factorización se puede escribir también así:

1/3.(x - 1/2)²